Brønsted Theory
According to the Brønsted theory, an acid is a proton donor, and a base is a proton acceptor. In an acid-base reaction, each side of the equilibrium has an acid and a base reactant or product, and these may be neutral species or ions.
| H-A + B:(–) |  |
A:(–) + B-H |
| (acid1) (base1) | (base2) (acid2) |
Structurally related acid-base pairs, such as {H-A and A:(–)} or {B:(–) and B-H} are called conjugate pairs. Substances that can serve as both acids and bases, such as water, are termed amphoteric.
| H-Cl + H2O |  |
Cl:(–) + H3O(+) |
| (acid) (base) | (base) (acid) |
| H3N: + H2O |  |
NH4(+) + HO(–) |
| (base) (acid) | (acid) (base) |
Useful General Principles: |
|---|
|
• The stronger the acid the weaker its conjugate base; the stronger the base the weaker its conjugate acid. • Acid-base equilibria always favor the weakest acid and the weakest base. |
Acidity
The relative strength of a group of acids may be evaluated by measuring the extent of reaction that each member undergoes with a common base. Water serves nicely as the common base for such determinations. Thus, for an acid H-A, its strength is proportional to the extent of its reaction with the base water, which is given by the equilibrium constant Keq.
H-A + H2O |
 | H3O(+) + A:(–) | 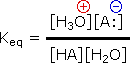 |
Since these studies are generally extrapolated to high dilution, the molar concentration of water (55.5) is constant and may be eliminated from the denominator. The resulting K value is called the acidity constant, Ka. Clearly, strong acids have larger Ka's than do weaker acids. Indeed, if HA is completely ionized in solution, Ka approaches infinity ( [HA] is nearly zero). Because of the very large range of acid strengths (greater than 1040), a logarithmic scale of acidity (pKa) is normally employed. Stronger acids have smaller or more negative pKa values than do weaker acids.
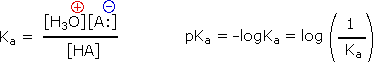
Examples of Brønsted Acid-Base Equilibria
| Acid-Base Reaction | Conjugate Acids | Conjugate Bases | Ka | pKa | |||
|---|---|---|---|---|---|---|---|
| HF + H2O |  | H3O(+) + F(–) | HF H3O(+) | F(–) H2O | 6.6*10-4 | 3.2 | |
| CH3CO2H + H2O |  | H3O(+) + CH3CO2(–) | CH3CO2H H3O(+) | CH3CO2(–) H2O | 1.77*10-5 | 4.75 | |
| HOCl + H2O |  | H3O(+) + ClO(–) | HOCl H3O(+) | ClO(–) H2O | 2.95*10-8 | 7.53 | |
| H2O2 + H2O |  | H3O(+) + HO2(–) | H2O2 H3O(+) | HO2(–) H2O | 2.5*10-12 | 11.6 | |
In all the above examples water acts as a common base, and the weakest acid and the weakest base will predominate, and will necessarily be on the same side of the equilibrium). Idealy, acid concentrations no larger than 0.1M should be used. Since water is amphoteric, it can undergo autoprotolysis as shown in the following equation. The autoionization is shown by Keq, and treating the water concentration as before, the acidity constant (Ka) for water is designated Kw (the water constant). The pH of pure water is therefore 7.0.
2 H2O  H3O(+) + OH(–) H3O(+) + OH(–) | 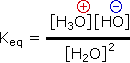 | Kw = [H3O(+)] [OH+] = 10-14 |
The range of strong acids that can be distinguished is limited. Thus acids that are stronger than the hydronium cation, H3O(+), and weak acids having conjugate bases stronger than hydroxide anion, OH(–), cannot be measured directly in water solution. If a strong acid (HA) has a Ka = 100, a 0.1M solution in water will ionize completely, giving a hydronium concentration of 100 and a [HA] concentration of 10-4. A similar solution of a 103 times stronger acid would be undetectably different due to this leveling effect of the solvent. The term leveling effect refers to the influence an amphoteric solvent such as water has on measurements of acidity and basicity. The strength of a strong acid is leveled by the basicity of the solvent, and the basicity of strong bases is likewise limited by solvent acidity.
Since many organic reactions either take place in aqueous environments ( living cells ), or are quenched or worked-up in water, it is important to consider how a conjugate acid-base equilibrium mixture changes with pH. A simple relationship known as the Henderson-Hasselbalch equation provides this information.
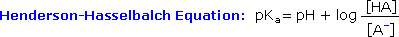
When the pH of an aqueous solution or mixture is equal to the pKa of an acidic component, the concentrations of the acid and base conjugate forms must be equal ( the log of 1 is 0 ). If the pH is lowered by two or more units relative to the pKa, the acid concentration will be greater than 99%. On the other hand, if the pH ( relative to pKa ) is raised by two or more units the conjugate base concentration will be over 99%. Consequently, mixtures of acidic and non-acidic compounds are easily separated by adjusting the pH of the water component in a two phase solvent extraction.
Basicity
In aqueous solution a base is a solute that increases the concentration of hydroxide ions. Metal alkoxides such as NaOCH3 and KOC(CH3)3 react with water giving solvated metal cations and alkoxide and hydroxide ions. These 100% ionizations make such compounds very strong bases. Many neutral bases are compounds of nitrogen. For such, we may write base-acid equilibria, which define a Kb and a corresponding pKb, as shown for ammonia in the first equation below. However, a more common procedure is to report the acidities of the conjugate acids of the bases, as shown in the second equation ( these conjugate acids are usually "onium" cations ). The pKa's reported for bases in this system are proportional to the base strength of the base. Note that in such relationships pKa + pKb = 14.
| Acid-Base Reaction | Conjugate Acids | Conjugate Bases | K | pK | |||
|---|---|---|---|---|---|---|---|
| NH3 + H2O |  | NH4(+) + OH(–) | NH4(+) H2O | NH3 OH(–) | Kb = 1.8*10-5 | pKb = 4.74 | |
| NH4(+) + H2O |  | H3O(+) + NH3 | NH4(+) H3O(+) | NH3 H2O | Ka = 5.5*10-10 | pKa = 9.25 | |
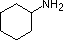
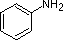
Most simple alkyl amines have pKa's in the range 9.5 to 11.0, and their water solutions are basic (have a pH of 11 to 12, depending on concentration). The first four compounds in the following table, including ammonia, fall into that category. The last six compounds (colored cells) are significantly weaker bases as a consequence of three factors. The first of these is the hybridization of the nitrogen. In pyridine the nitrogen is sp2 hybridized, and in nitriles (last entry) an sp hybrid nitrogen is part of the triple bond. In each of these compounds (shaded red) the non-bonding electron pair is localized on the nitrogen atom, but increasing s-character brings it closer to the nitrogen nucleus, reducing its tendency to bond to a proton. Secondly, aniline and p-nitroaniline (first two green shaded structures) are weaker bases due to delocalization of the nitrogen non-bonding electron pair into the aromatic ring (and the nitro substituent). This is the same delocalization that results in activation of a benzene ring toward electrophilic substitution. Indeed, aniline is a weaker base than cyclohexyl amine by roughly a million fold, the same factor by which phenol is a stronger acid than cyclohexanol. This electron pair delocalization is accompanied by a degree of rehybridization of the amino nitrogen atom, but the electron pair delocalization is probably the major factor in the reduced basicity of these compounds. A similar electron pair delocalization is responsible for the very low basicity (and nucleophilic reactivity) of amide nitrogen atoms (last green shaded structure).
| Compound | 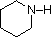 |
 |
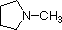 |
NH3 |  |
 |
 |
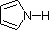 |
 |
CH3C≡N |
|---|---|---|---|---|---|---|---|---|---|---|
| pKa (onium) | 11.0 | 10.7 | 10.7 | 9.3 | 5.2 | 4.6 | 1.0 | 0.0 | -1.0 | -10.0 |
Lewis Theory
According to the Lewis theory, an acid is an electron pair acceptor, and a base is an electron pair donor. Lewis bases are also Brønsted bases; however, many Lewis acids, such as BF3, AlCl3 and Mg2+ , are not Brønsted acids. The product of a Lewis acid-base reaction, is a neutral, dipolar or charged complex, which may be a stable covalent molecule. As shown at the top of the following drawing, coordinate covalent bonding of a phosphorous Lewis base to a boron Lewis acid creates a complex in which the formal charge of boron is negative and that of phosphorous is positive. In this complex, boron acquires a neon valence shell configuration and phosphorous an argon configuration. Two examples of Lewis acid-base equilibria that play a role in chemical reactions are shown in equations 1 & 2 below.
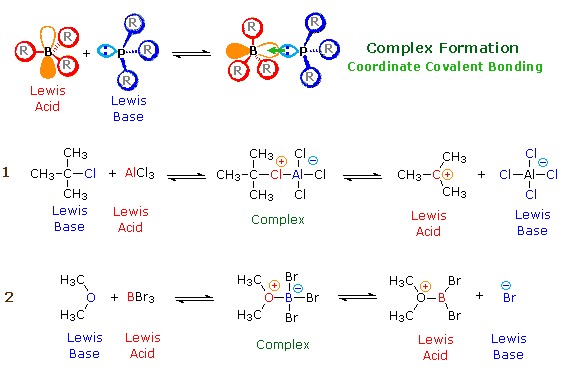
In the first example, an electron deficient aluminum atom bonds to a covalent chlorine atom by sharing one of its non-bonding valence electron pairs, and thus achieves an argon-like valence shell octet. Because this sharing is unilateral (chlorine contributes both electrons), both the aluminum and the chlorine have formal charges, as shown. If the carbon chlorine bond in this complex breaks with both the bonding electrons remaining with the more electronegative atom (chlorine), the carbon assumes a positive charge. We refer to such carbon species as
carbocations. Carbocations are also Lewis acids, as the reverse reaction demonstrates. If the substituents (R) on these atoms are not large, the complex will be favored at equilibrium. However, steric hindrance of bulky substituents may prohibit complex formation. The resulting mixture of non-bonded Lewis acid/base pairs has been termed "frustrated", and exhibits unusual chemical and catalytic behavior. The combination of P(t-Butyl)3 and B(C6F5)3 is an example.
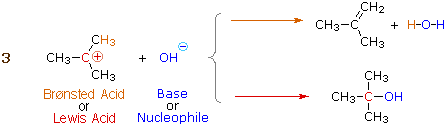
Many carbocations (but not all) may also function as Brønsted acids. Equation 3 illustrates this dual behavior for (CH3)3C(+) ; the Lewis acidic site is colored red and three of the nine acidic hydrogen atoms are colored orange. In its Brønsted acid role the carbocation donates a proton to the base (hydroxide anion), and is converted to a stable neutral molecule having a carbon-carbon double bond.
A terminology related to the Lewis acid-base nomenclature is often used by organic chemists. Here the term electrophile corresponds to a Lewis acid, and nucleophile corresponds to a Lewis base.
Electrophile: An electron deficient atom, ion or molecule that has an affinity for an electron pair, and will bond to a base or nucleophile.
Nucleophile: An atom, ion or molecule that has an electron pair that may be donated in bonding to an electrophile (or Lewis acid).
Some confusion in distinguishing basicity (base strength) and nucleophilicity (nucleophile strength) is inevitable. Since basicity is a less troublesome concept; it is convenient to start with it.
Basicity refers to the ability of a base to accept a proton. Basicity may be related to the pKa of the corresponding conjugate acid. The strongest bases have the weakest conjugate acids and vice versa. In an acid-base equilibrium the weakest acid and the weakest base will predominate and they will necessarily be on the same side of the equilibrium.
Solvents such as acetic acid, acetonitrile and nitromethane are often used for studying very strong acids. Likewise, very weakly acidic solvents such as dimethylsulfoxide (DMSO), acetonitrile, toluene, amines and ammonia may be used to study the acidities of very weak acids. Measurements in these solvents may be extrapolated to water and many have large uncertainties. For both acids and bases, the reported pKa values extrapolated to water are approximate. A table of some basic reagents is shown below. The range of basicities is remarkable, covering over fifty powers of ten!
| Base | I (–) | Cl (–) | H2O | CH3CO2(–) | RS(–) | CN(–) | RO(–) | NH2(–) | CH3(–) |
|---|---|---|---|---|---|---|---|---|---|
| Conj. Acid | HI | HCl | H3O(+) | CH3CO2H | RSH | HCN | ROH | NH3 | CH4 |
| pKa | -9 | -7 | -1.7 | 4.8 | 8 | 9.1 | 16 | 33 | 48 |

Nucleophilicity is a more complex property. It commonly refers to the rate of substitution reactions at the halogen-bearing carbon atom of a reference alkyl halide, such as CH3-Br. Thus the nucleophilicity of the Nu:(–)reactant in the following substitution reaction varies as shown in the chart below. The reactivity range encompassed by these reagents is over 5,000 fold, thiolate being the most reactive. Clearly, there are significant differences between these nucleophilicities and the basicities discussed above.
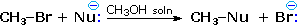 |
|---|
Nucleophilicity: CH3CO2(–) < Cl(–) < Br(–) < N3(–) < CH3 O(–) < CN(–) < I(–) < CH3S(–) |
 |
| Some useful trends have been documented: (i) For a given element, negatively charged species are more nucleophilic (and basic) than are equivalent neutral species. (ii) For a given period of the periodic table, nucleophilicity (and basicity) decreases on moving from left to right. (iii) For a given group of the periodic table, nucleophilicity increases from top to bottom ( i.e. with increasing size), although there is a solvent dependence due to hydrogen bonding. Basicity varies in the opposite manner. |
For two or more molecules incorporating nucleophilic atoms of the same kind and charge, the stronger base is usually the stronger nucleophile. Thus, 2,2,2-trifluroethoxide (pKa 12) is a weaker base and nucleophile than ethoxide (pKa 16). A notable exception to this rule occurs when a vicinal (adjacent) atom carries a non-bonding electron pair. Two common examples of this exception, called the alpha effect, are hydroxide ion (pKa 15.7) compared with hydroperoxide ion (pKa 11.6), and ammonia (pKa 9.3) compared with hydrazine (pKa 8.0). In each of these pairs the weaker base is the stronger nucleophile.
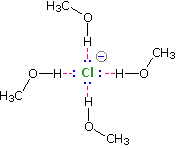
Solvation of nucleophilic anions markedly influences their reactivity. The nucleophilicities cited above were obtained from reactions in methanol solution. Polar, protic solvents such as water and alcohols solvate anions by hydrogen bonding interactions, as shown in the diagram on the right. These solvated species are more stable and less reactive than the unsolvated "naked" anions. Polar, aprotic solvents such as DMSO (dimethyl sulfoxide), DMF (dimethylformamide) and acetonitrile do not solvate anions nearly as well as methanol, but provide good solvation of the accompanying cations. Consequently, most of the nucleophiles discussed here react more rapidly in solutions prepared from these solvents. Such solvent effects are more pronounced for small basic anions than for large weakly basic anions. Thus, for reaction in DMSO solution we observe the following reactivity order:
| Nucleophilicity: I(–) < Br(–) < Cl(–)~ N3(–) < CH3CO2(–) < CN(–) ~ CH3S(–) < CH3O(–) |
 |
|---|
Unlike the order in methanol (shown above), this ranking is roughly the order of increasing basicity. Neutral bases like ammonia and simple primary and secondary amines have similar basicities (pKa = 9 to 11) and are also good nucleophiles. In reactions with methyl bromide in methanol their nucleophilicity is greater than Cl(–) and less than N3(–). In slightly basic aprotic solvents they react with moderate electrophiles such as alkyl halides ( Cl, Br and I ) and carbonyl groups (aldehydes, ketones, esters and anhydrides), giving quaternary salts from the former, and imines, enamines and amides from the latter. Tertiary amines and bulky secondary amines are poorer nucleophiles and behave exclusively as bases.
Solvent Effects
Acids
The ionization of a group of acids in a given solvent may be used as a measure of acid strength, and in such cases the solvent serves as a common reference base. The determination of Ka and pKa values for any solvent system may be carried out in the same way as in water; however, the acidities obtained for a group of acids measured in different solvents will generally be different, both in the numerical value for each, and sometimes in relative order.
| A–H an acid | + | Sol: solvent |
 |
A:(–) conjugate base |
+ | Sol–H(+) conjugate acid |
There are several factors which influence acidity measurements made in water and other solvents. These are:
2. The conjugate acid from the solvent is a cation that is stabilized by association with other solvent molecules, a phenomenon called solvation.
3. The conjugate base of the acid is an anion, that in most cases is also stabilized by solvation.
| ||||||||||||||||||||||||||||
| * Perchloric acid and trifluoromethanesulfonic acid are both completely ionized in water and DMSO. The pKa value of –10 is approximate, and is intended to reflect the high degree of dissociation. |
All three solvents have fairly high dielectric constants, but water (ε = 80) is significantly greater than DMSO (ε = 46.7) or acetonitrile (ε = 37.5). The greater acidity (lower pKa) of the last four compounds in water might be attributed to the dielectric difference; however, the superior anion solvation provided by water is considered to be the major factor. Both DMSO and acetonitrile are poor anion solvation solvents, consequently the ionization equilibrium shown above will be shifted to the left.
It is informative to focus first on the pKa differences between water and DMSO. We do this because water and DMSO have similar basicities, so stabilization of the solvent conjugate acid species should not differ substantially. HBr and HCl display pKas in DMSO that are roughly 9 to 10 powers of ten more positive than in water, and the weaker second period acid HF shows an even greater change (pKa = 3.17 in water & 15 in DMSO). The conjugate bases of these acids are all single atom anions. Because the negative charge is localized, anion stabilization by solvation is probably the most important factor in establishing the position of these equilibria. In contrast, the conjugate bases from sulfuric acid and trifluoroacetic acid are internally stabilized by charge delocalization over two or three oxygen atoms. The importance of solvation is therefore less important, and the shift in acidity in DMSO is reduced to 4 powers of ten.
When acetonitrile is the solvent, the measured pKas of these acids show a further increase, and even the strongest acids are not completely dissociated. This change may be attributed in large part to diminished solvation of the solvent conjugate acid, which is the chief cation species in dilute solutions. Since both the cationic and anionic species from acidic ionization are poorly stabilized by solvation, the dissociation equilibrium lies far to the left (little ionization).
| Compound | H2O | DMSO | CH3CN |
|---|---|---|---|
| C2H5OH | 17 | 29 | 42 |
| CF3CH2OH | 12.4 | 23.5 | 33.5 |
| C6H5C≡CH | 19 | 29 | 40.6 |
| C4H9SH | 10.5 | 17 | 28.6 |
| CH3CO2H | 4.8 | 12.8 | 22.3 |
| C6H5CO2H | 4.2 | 11.1 | 20.7 |
| C6H5OH | 10 | 18 | 26.6 |
| C6H5SH | 6.6 | 10.3 | 20.6 |
Most organic compounds are much weaker acids than the strong acids discussed above. It is therefore of interest to determine the changes in acidity that take place when such compounds are examined in the same three solvents. The first four compounds in this table (shaded light green) are weak acids having conjugate bases in which the charge is localized on a single atom ( O, C & S ). Changing the solvent from water to DMSO decreases the acidity by 10 to 12 powers of ten for second period atoms ( C & O ), and by 6.5 for the third period sulfhydryl acid. Just as in the more acidic cases treated above, solvation of the conjugate base anions is an important stabilizing factor in water, although the lower charge density on sulfur reduces its significance. The further increase in pKa that occurs in acetonitrile solutions, relative to DMSO, is fairly uniform (10 to12 units) and a bit larger than the shift found for the strong acids.
The last four compounds (shaded blue) have conjugate bases stabilized by charge delocalization. Here, the decrease in acidity going from water to DMSO is lowered to 7 to 8 powers of ten for oxygen and is less than 4 for sulfur. As noted previously, charge delocalization within an anion reduces the importance of solvation stabilization. The increase in pKa found for acetonitrile solutions remains roughly the same, and may be attributed to poor solvation in this solvent.
With the exception of the acetylene derivative, the previous compounds are all heteroatom acids. Similar measurements for a group of activated carbon acids show agreement with the previous analysis, and illustrate the manner in which anionic charge delocalization reduces the pKa difference between water and DMSO measurements. Note the near identity of the second and third examples in the following table. As expected, the pKa increase in going to acetonitrile from DMSO remains roughly constant (ca. 11).
| Compound | H2O | DMSO | CH3CN |
|---|---|---|---|
| (CH3CO)2CH2 | 9 | 13.3 | 24.4 |
| (N≡C)2CH2 | 11.2 | 11.2 | 22.2 |
| (C6H5SO2)2CH2 | 11.6 | 12.2 | 23.2 |
| (C2H5OCO)2CH2 | 13.5 | 16.4 | 27.8 |
| C4H4CH2 cyclopentadiene |
15.0 | 18.0 | 31.2 |
Bases
The most common notation for reporting relative base strengths of a neutral base (B:) is in terms of the pKa's of the corresponding conjugate acids ( these conjugate acids are often called "onium" cations ). The following equation shows the equilibrium involved in this relationship. Note that strong bases will have weakly acidic conjugate acids, so the pKa is proportional to the base strength of the neutral base.
| B–H(+) conjugate acid | + | Sol: solvent |  | B: a base |
+ | Sol–H(+) conjugate acid |
The previously defined factors that influenced acidity may now be reexamined for this new equilibrium.
1. Ions are present on both sides of the equation. Consequently, differences in the solvent dielectric constant should be a relatively unimportant factor.
2. The base and solvent conjugate acid cations are both stabilized by solvation. This will be a critical factor, and is related to solvent basicity.
3. There are no anions in the above equation; however charge neutralization requires a counter anion. Since the same anion will be present on both sides of the equation, its influence on this equilibrium will be canceled.
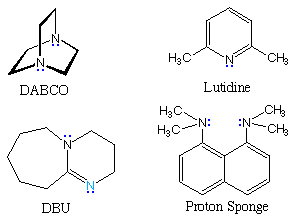
The following table gives pKa values for some important nitrogen bases, some structures for which are shown to its right. In the triethylamine and DABCO examples at the top of the table, the cationic charge is relatively localized on a single nitrogen atom. The charge in lutidine may be delocalized onto ring carbons at the cost of aromatic stabilization. The last three examples are compounds in which the charge is delocalized by resonance (protonation occurs at the light blue nitrogen) or internal hydrogen bonding (the proton sponge).
In contrast to the earlier examples of acid pKas, the values for these ammonium cations are nearly identical in water and DMSO solvents. Indeed, the fact that most of the DMSO pKas are a bit lower than their water counterparts suggests that DMSO is slightly more basic than water. In acetonitrile all the pKa values are about 10 units higher than the DMSO values.
|  |
|---|
The influence of solvent on acidity and basicity noted above may cause unexpected changes in simple acid-base equilibria. If acetic acid and triethyl amine are mixed together in water, a rapid proton transfer takes place to give nearly quantitative formation of triethyl ammonium acetate. The conjugate acids differ in strength by 106 and the weakest is favored at equilibrium. When the same two compounds are combined in DMSO solution there is negligible proton transfer, since acetic acid is now over 103 times weaker an acid than the triethyl ammonium cation.
Hammett Acidity Function
Ionization measurements of aqueous solutions of acids (and bases) are generally limited to a pH range of 1.5 to 13. Relative values of stronger acids (and bases) require the use of other solvents, and due to variations in dielectric constants, solvation, and other deviations from ideality, consistant relationships are not achieved. A remedy for this situation was proposed by Louis Hammett (Columbia University). Hammett suggested using a series of weak indicator bases wherein the [B]/[BH+] ratio could be determined colorimetrically due to a distinctively colored conjugate acid. When the ratio of [B] to [BH+] becomes especially small and experimentally impossible to measure accurately, a different, less basic indicator, overlapping the first, would serve to extend the acidity range. Additional weaker indicator bases would then allow one to leapfrog across the acidity scale, extending it roughly 1010 fold. To this end, an acidity function, Ho, was defined as shown by the following equation.
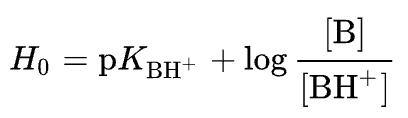
| autoprotolysis 2 H2SO4  H3SO4(+) + HSO4(–) H3SO4(+) + HSO4(–) |
|
The following tables list some of Hammett's indicator bases and the Ho's of some very strong acids or "super acids". The pKa of the indicator bases were determined in aqueous solutions of the strong acids H2SO4 and HClO4. Ho values were determined in anhydrous sulfuric acid, and those stronger than -16 are estimates.
|
|
|---|
Strong Bases
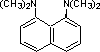
Organic chemists need bases of varying strength as reagents tailored to the requirements of specific reactions. Neutral nitrogen compounds can cover a basicity range of roughly 1010, as shown in the following table. Pyridine is commonly used as an acid scavenger in reactions that produce mineral acid co-products. Its basicity and nucleophilicity may be modified by steric hindrance, as in the case of lutidine (pKa=6.3), or resonance stabilization, as in the case of 4-dimethylaminopyridine (pKa=9.2). Hünig's base is relatively non-nucleophilic (due to steric hindrance), and like DBU is often used as the base in E2 elimination reactions conducted in non-polar solvents. Barton's base is a strong, poorly-nucleophilic, neutral base that serves in cases where electrophilic substitution of DBU or other amine bases is a problem.
| Base Name | Pyridine | Lutidine | DABCO | DMAP | Triethyl Amine | Hünig's Base | DBU | Proton Sponge | Barton's Base |
|---|---|---|---|---|---|---|---|---|---|
| Formula | 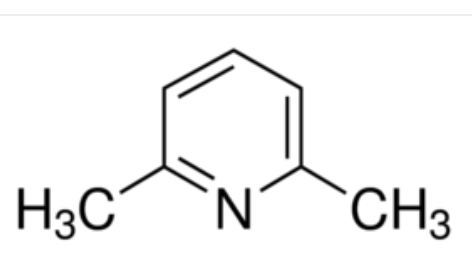 | 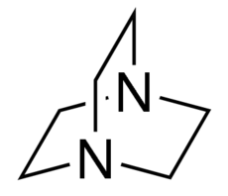 | 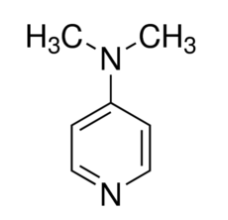 |
(C2H5)3N | 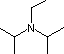 |
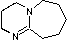 |  |
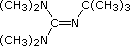 |
|
| pKa (onium) | 5.3 | 6.27 | 8.8 | 9.2 | 10.7 | 11.4 | 12 | 12.4 | 14 |
The strongest bases available to organic chemists are alkali metal alkoxide salts such as potassium tert-butoxide (pKa = 16 to 19), alkali metal alkyls such as Grignard reagents, n-butyl lithium and dimsyl sodium (pKa = 28 to upper 40s), and amide salts of alkali metals, such as LDA (pKa = 30 to 40) and sodium hydride (pKa ~ 42). These powerful bases are all potential nucleophiles (some more than others) and have partially ionic bonds to the metals. Bases in these pKa ranges are used to convert weak C-H acids into useable carbanionic-metal reagents.
* DMSO = Dimethylsulfoxide |
Some examples of alkylmetal preparations, together with similar amide metal bases are shown in the following equations. In all cases inert solvents such as benzene, cyclohexane, tetrahydrofuran and ether are used. Since these reactions proceed to completion, equilibrium arrows are not drawn. Methyl Magnesium Iodide: CH3I + Mg —> CH3MgI (ether solution) Butyl Lithium: 2 Li + C4H9X —> C4H9Li + LiX (where X = Cl, Br) Trityl Sodium*: (C6H5)3CCl + 2 Na —> (C6H5)3CNa + NaCl Dimsyl Sodium: CH3SOCH3 + NaH —> CH3SOCH2Na + H2 LDA: [(CH3)2)CH]2NH + C4H9Li —>[(CH3)2)CH]2NLi + C4H10 LiHMDS: {(CH3)3Si}2NH + C4H9Li —> {(CH3)3Si}2NLi + C4H10 *This anion is red and serves as an indicator. It is also a one electron reductant. Nitrile Alkylation: RCH2CN + LDA —> RCHCNLi + {(CH3)2)C}2NH ; RCHCNLi + R'X —> R'RCHCN + LiX Aldehydes, ketones and esters having activated C-H groups may be similarly converted to their conjugate bases, followed by alkylation or addition to electrophilic functions. |
*TMP = 2,2,6,6-Tetramethylpiperidine *HMDS = Bis(trimethylsilyl)amine |
Nonionic Superbases
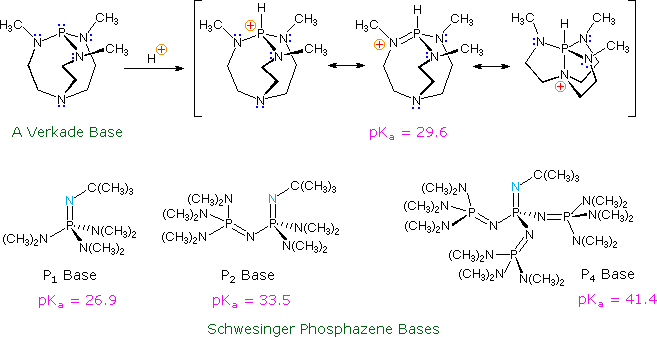
Recently, a new class of non-metallic, poorly nucleophilic, neutral bases have been prepared and studied. Some examples are shown in the following diagram.
The basic site in the Verkade base is the phosphorous atom, the conjugate acid being stabilized by transannular bonding to nitrogen. The strength of these bases may be modified by substituents on the flanking nitrogens. The Schwesinger phosphazene bases increase their strength as additional phosphazene units are added in conjugation with the basic site (the light blue nitrogen atom). All the pKas for these bases are measured in acetonitrile.
Kinetic Acidity
The most common acid-base terminology, pKa , reflects an equilibrium acidity, extrapolated or normalized to water. In the following equation a base, B:(–) M(+), abstracts a proton from an acid, H-A, to form a conjugate acid - base pair (A:(–) M(+) & B-H). The rate of the forward proton abstraction is k f , and the reverse rate of proton transfer is k r. This kind of equilibrium is usually characterized by an equilibrium constant, Keq, which is the ratio of the rate constants (k f / k r). If H-A is a weaker acid than H-B the equilibrium will lie to the left, and Keq will be smaller than 1.
| H-A + B:(–) M(+) | 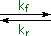 |
A:(–) M(+) + B-H |
| (acid1) (base1) | (base2) (acid2) |
In cases where H-A is very much weaker than H-B, Keq may be too small to measure, but it may be possible to determine the rate of the forward proton abstraction under certain circumstances. If an isotopically labeled conjugate acid of the base is used as a solvent for the reaction (B-D in the following equations), then any proton abstraction that occurs will be marked by conversion of H-A to D-A. The green shaded top equation shows the initial loss of the proton, and the second equation describes the rapid deuteration of the intermediate conjugate base, A:(–). As these reactions proceed, the H-A reactant will be increasingly labeled as D-A, and the rate of isotope exchange will indicate the kinetic acidity of H-A. It is assumed that kinetic acidity is roughly proportional to equilibrium (thermodynamic) acidity, but this is not always true.
| solvent = B-D | ||
| H-A + B:(–) M(+) |  |
A:(–) M(+) + B-H |
| D-A + B:(–) M(+) |  |
A:(–) M(+) + B-D |
The following diagram provides an instructive example of these principles. The first equation, in the yellow shaded box, provides important information about heavy water (deuterium oxide), which will be used as a solvent for our experiment. Heavy water is similar to water in many respects, but is 10% more dense and a ten-fold weaker acid. A 1 molar concentration of sodium deuteroxide will serve as the base, and an equimolar quantity of 3,3-dimethyl-1-butyne will serve as the weak acid. The most acidic hydrogen in this hydrocarbon (colored red) is at C-1. In practice, we would need to use a co-solvent to completely dissolve the hydrocarbon in the heavy water, but this has been omitted in order to simplify the discussion.
The second equation describes the essential changes expected on combining these reactants in the heavy water solvent. Since the terminal alkyne is a much weaker acid than heavy water, acid-base equilibria do not favor its conjugate base. Nevertheless, if the acetylide anion is formed, even in low concentration, it should react quickly by abstracting a deuterium from a neighboring deuterium oxide molecule. The result would be an observable exchange of deuterium for hydrogen, testifying that an acid-base reaction has occurred.

The green shaded box contains equations that help us to interpret the experimental results. In order to evaluate the equilibrium acidity of the substrate, we would need to measure the equilibrium constant Keq for the initial acid-base equilibrium, shown at the top of the shaded box. Since we know the Ka 's of 3,3-dimethyl-1-butyne and heavy water, we can estimate Keq by dividing the former (10 -25) by the latter (10 -17). This calculation reveals a Keq that would be difficult to measure directly because of its small magnitude (10 -8). Indeed, the equilibrium concentration of acetylide anion is estimated to be only 2*10 -10 M.
If we examine this experiment from the viewpoint of kinetics, easily observable evidence of terminal alkyne acidity is obtained. The last three rows of equations in the green shaded box make this clear. Since Keq is the ratio of forward and reverse rate constants, it is possible to draw conclusions about the rate of terminal proton abstraction from the alkyne. This leads to the conclusion that reasonably rapid hydrogen-deuterium exchange will occur, even though the acetylide anion is never present in concentrations exceeding 10 -9 M.
This example also demonstrates the limits of the isotope exchange approach. The 3,3-dimethyl-1-butyne substrate also has nine other hydrogen atoms (colored orange) that do not exchange with deuterium under these conditions. We know that these hydrogens are much less acidic (Ka ca. 10 -48), and it is interesting to consider their potential participation in acid-base reactions by the previous analysis. The estimated Keq for such carbanion formation is ca.10 -30, taking into account the nine-fold increase in concentration. This implies a concentration of one carbanion in every 109 liters of solution. The kinetic analysis is equally discouraging. The forward rate constant is estimated to be 10 -20 Ms-1. The time required to exchange half these hydrogens for deuterium would therefore be about 100 centuries!
In order to study the kinetic acidity of extremely weak acids (pKa's = 30 to 50) it is necessary to use much stronger bases, which of course have much weaker conjugate acids. Amide anions (pKa's = 26 to 36) have been used for this purpose.
By comparing the rates of hydrogen exchange for different compounds under identical conditions, tables of relative kinetic acidities may be assembled. An interesting example of such a study has been reported for a group of nitroalkanes having acidic α-hydrogens. Removal of an α-hydrogen by a base generates a conjugate base called an aci-anion, as shown here.
Compared with the terminal alkyne discussed above, such nitroalkanes are relatively strong C-H acids. Since they are stronger acids than water, the kinetic exchange experiments must be conducted under milder conditions than those used for the terminal alkyne. This is achieved by using smaller base concentrations and lowering the temperature of the exchange reaction. Accurate pKa's of 2-nitropropane, nitroethane and nitromethane may be measured directly in aqueous solution. These kinetic and equilibrium acidities are listed in the table on the right. Note that for these three compounds, kinetic acidity changes in an opposite fashion to equilibrium acidity. The kinetic order seems to reflect steric hindrance and carbanion stability; whereas, the equilibria favor increased substitution of the aci-anion double bond. |
|
Base-catalyzed isotope exchange studies of compounds incorporating more than one set of acidic hydrogens provides additional insight concerning the creation and use of nucleophilic conjugate bases. Ketones provide many examples of regioisomeric enolate base formation, and the following diagram shows two such cases. As noted in the nitroalkane study, hydrogens on an α-methyl group are exchanged more rapidly than those on more substituted α-carbon atoms. The equations in the diagram show only the initial product from a single exchange. These products have additional α-hydrogens which are also exchanged by subsequent reactions of this kind, so that complete replacement of all α-hydrogens by deuterium takes place in a short time.
The relative stability of the resulting enolates increases with substitution of the enolate double bond. Equations showing the equilibrium concentrations of these isomeric enolates will be displayed by clicking the Toggle Equations button. In order to determine enolate anion equilibria for these ketones, the bulky strong base sodium Bis(trimethylsilyl)amide (pKa = 26) was used.
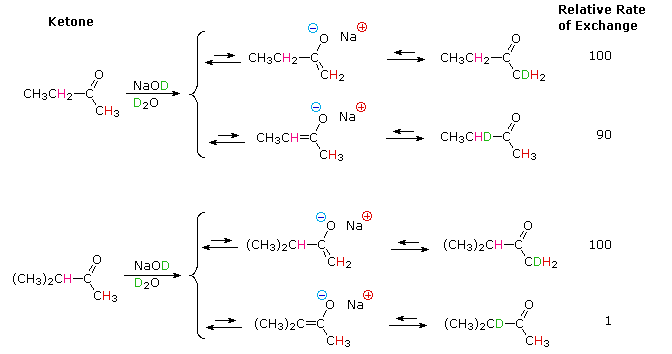
By clicking the Toggle Equations button a second time, the relative rates of α-hydrogen exchange for some substituted cyclohexanones will be displayed above. Once again, less substituted α-carbons exchange more rapidly, but more highly substituted enolates are found to predominate under equilibrium conditions. A third click of the Toggle Equations button will display an energy profile for the 2-methylcyclohexanone case, which should clarify the distinction between kinetic and equilibrium acidity. Two other examples are also shown. These displays may be cycled repeatedly.
Most carbon acids yield conjugate bases that are stabilized by charge delocalization onto neighboring heteroatoms. This resonance stabilization requires significant structural reorganization of the initial compound, which in turn imposes an energy barrier that retards the rate of proton abstraction. For example, the alpha-carbon of a ketone or ester must undergo rehybridization as the enolate anion is formed. The stereoelectronic demands of this change were described above, and it is not surprising that enolate anion formation is much slower than equivalent proton transfers between alcohols and other hydroxylic compounds. Deprotonation rates of phenol and nitromethane, compounds with nearly identical pKa's (10.0), provide an instructive example of this structural reorganization factor. The acidic proton in phenol is bound to oxygen, so deprotonation requires little structure change and is very fast. Nitromethane is a carbon acid. Deprotonation to an aci-anion involves considerable structural change, and is a million times slower than phenolate formation. These structural changes are illustrated in the following diagram.
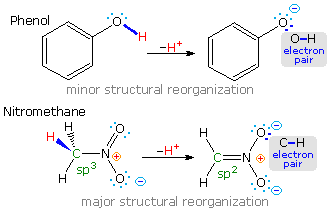
Note that the O-H electron pair in phenol remains largely on oxygen in the corresponding conjugate base, whereas the C-H electron pair in nitromethane is predominantly shifted to oxygen in its conjugate base (colored blue). The trends outlined here are a bit oversimplified, since solvent and cation influences have been ignored.
This page is the property of William Reusch. Comments, questions and errors should be sent to:
whreusch@msu.edu.